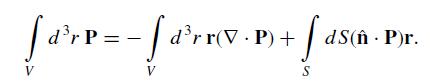
Assume that (r) and G(r) both go to zero faster than 1 r as r (a) Let F and G 0 Show that d 3 r F G 0 (b) Let F and G 0 Show that d 3 r F G 0 (c) Begin with the vector with components j (P j G) and prove that dr drrv V V dr r(V P) dS( P)r S...

a By direction substitution The last integral is zero with the stated conditio ...

Assume that (r) and |G(r)| both go to zero faster than 1/r as r . (a) Let

Question:

Assume that ϕ(r) and |G(r)| both go to zero faster than 1/r as r →∞.

(a) Let F = ∇ϕ and ∇ · G = 0. Show that ∫ d³r F · G = 0.

(b) Let F = ∇ϕ and∇ ×G = 0. Show that ∫ d³r F × G = 0.

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For book-img-for-question

Modern Electrodynamics

ISBN: 9780521896979

1st Edition

Authors: Andrew Zangwill

See More Books

Question Posted: Feb 02, 2023 01:17 AM

See More Questions

Let f : R R. Prove that f is continuous on R if and only if f-1 (I) is open in R for every open interval I.
Let f : A and g : B C and define g o f : A C by (g o f)(x) := g(f(x)). a) Show that if f, g are 1-1 (respectively, onto), then g o f is 1-1 (respectively, onto). b) Prove that if f is 1-1 from A...
Let f : A B and g : B C be functions. (a) Show that if g f is injective, then f is injective. (b) Show that if g f is surjective, then g is surjective.
When would you suggest that an organization engage in workflow analysis?
For Table 3.6, the regression equation for the 50 states and D.C. relating y = murder rate and x = percent of people who live below the poverty level is = -4.1 + 0.81x . For D.C., x = 17.4 and y =...
Calculate the angular velocity of an electron orbiting a proton in the hydrogen atom, given the radius of the orbit is 0.530 x 10 -10 m. You may assume that the proton is stationary and the...
An investigator is considering two blocking schemes for a $2^{4}$ design with 4 blocks. The two schemes are listed below. Scheme 1: $B_{1}=134, B_{2}=234$ Scheme 2: $B_{1}=12, B_{2}=13, B_{3}=1234$...
1. Cash inflows from operating activities come from a. Payment for raw materials. b. Collection of sales revenues. c. Gains on the sale of operating equipment. d. Issuing capital stock. e. Issuing...
On May 1, 2022, Cullumber Company purchased the copyright to Bramble Corp. for $134400. It is estimated that the copyright will have a useful life of 4 years. What would be the amount of amortization...
Kara is opening up a new daycare business in her home. She needs $6500 to purchase toys and a backyard playset. Kara makes a 10% down payment and finances the balance with a 48-month fixed...
Compute the unit normal vector n to the ellipsoidal surfaces defined by constant values of Check that you get the expected answer when a = b = c. (x, y, z) = V + 6 2
Without using vector identities, prove that: (a) f (r r) = (r r). (b) [A(r) r] = 0. (c) dQ = (ds )Q where dQ is a differential change in Q and ds is an element of arc length.
List the types of costs incurred when employees are laid off. What costs are difficult to estimate in monetary terms? Suppose that a firm is facing a downturn in business, each employee has skills...
Introduction: In the late 1950s and early 1960s, an anthropologist, C.M. Turnbull, travelled to the Ituri Forest in the present-day country of the Democratic Republic of the Congo (formerly Zaire) to...
Gregor Olson works at the National Bank branch in Copenhagen. According to the banks records, there is currently an outstanding loan of $380,000 to Danville Bus Services, a company that schedules...
In the current legal and ethical landscape, it is unclear who would be held accountable in such a situation. The responsibility could potentially fall on the creators of the AI system, the healthcare...
Identify another instance in the body that makes use of the chemical topic of acids and bases, and then explain the topic's significance.
Hannah's organization is implementing a new approach to user authentication that relies upon SAML. She would like to protect against eavesdropping on this traffic and also ensure that SAML traffic is...
Repeat Exercise 6 using the clamped cubic splines constructed in Exercise 8. In Exercise 6 a. f (x) = e2x ; approximate f (0.43) and f' (0.43). b. f (x) = x4 x3 + x2 x + 1; approximate f (0) and...
Explain five different cases of income exempt from tax with clear examples.
How many milliliters of 0.800 M KOH should be added to 5.02 g of 1,5-pentanedioic acid (C 5 H 8 O 4 , FM 132.11) to give a pH of 4.40 when diluted to 250 mL?
Calculate the pH of a 0.010 M solution of each amino acid in the form drawn here. H2N NH2 NH2 NH C=0 CH2 CH2 S CH, CH, CH2 CH2 (a) H;NCHCO, (b) H&NCHCO, (c) H,NCHCO, Glutamine Cysteine Arginine
(a) Draw the structure of the predominant form (principal species) of 1,3-dihydroxybenzene at pH 9.00 and at pH 11.00. (b) What is the second most prominent species at each pH? (c) Calculate the...
Evaluation of the correlation between emotional intelligence and Job satisfaction objectives To evaluate the correlation between self-awareness and job satisfaction among Total energies employees To...
What's job satisfaction largely based on? What is not a major determinant of job satisfaction?
Define the concept of job satisfaction, including the personal characteristics that impact job satisfaction. Propose two tactics/strategies an organization should pursue to raise the job satisfaction...

Assume that (r) and |G(r)| both go to zero faster than 1/r as r . (a) Let

Question:

[d³r² = - [d³rrv. V V d³r r(V. P) +dS(-· P)r. S

Step by Step Answer:

a By direction substitution The last integral is zero with the stated conditio...View the full answer

Modern Electrodynamics

Students also viewed these Engineering questions