(a) An object moves along a straight line. Its displacement from its initial position is s(t). Show that its velocity v(t) is given by s´(t). The acceleration of the object is a(t). Show that

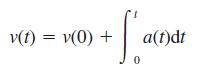
and deduce that a(t) = s´´(t).

(b) A ball-bearing travels along a track with velocity v(t) m s^–1 given by the function v(t) = 8 – 0.5t² where t is the time in seconds. Calculate the exact distance travelled by the ball-bearing over the time periods (0, 4) and (4, 5). Obtain also the formula for the acceleration of the ball bearing at time t.

v(t) = v(0) + S': 0 a(t)dt