A colony of insects is observed at regular intervals and comprises four age groups containing n₁, n₂, n₃, n₄ insects in the groups. At the end of an interval, of the n₁ in group 1 some have died and (1 – β₁)n₁ become the new group 2. Similarly (1 – β₂)n₂ of group 2 become the new group 3 and (1 – β₃)n₃ of group 3 become the new group 4. All group 4 die out at the end of the interval. Groups 2, 3 and 4 produce α₂n₂, α₃n₃ and α₄n₄ infant insects that enter group 1. Show that the changes from one interval to the next can be written as

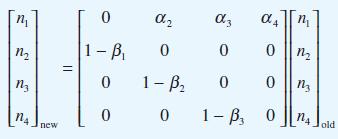
Take α₃ = 0.5, α₄ = 0.25, β₁ = 0.2, β₂ = 0.25 and β₃ = 0.5. Try the values α₂ = 0.77, 0.78, 0.79 and check whether the population grows or dies out over many intervals starting from an initial population

Find the eigenvalues in the three cases and check the magnitudes of the eigenvalues. Is there any connection between survival and eigenvalues? Realistic populations can be modelled using this approach; the matrices are called Leslie matrices.