Consider again the design of the milk carton discussed in Example 8.35. Show that if the overlap used in its construction is x mm instead of 5 mm, the objective function that must be minimized is

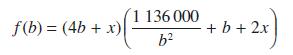
Show that when x = 0, the optimal value for b is b*₀ = 10(568)^1/3. The optimal value b* depends on x. Obtain the Maclaurin series expansion for b* as far as the term in x² and discuss the effect of the overlap size on the design of the carton.

Data from Example 8.35

A milk retailer wishes to design a milk carton that has a square cross-section, as illustrated in Figure 8.39(a), and is to contain two pints of milk (2 pints ≡ 1.136 litres). The carton is to be made from a rectangular sheet of waxed cardboard, by folding into a square tube and sealing down the edge, and then folding and sealing the top and bottom. To make the resulting carton airtight and robust for handling, an overlap of at least 5 mm is needed. The procedure is illustrated in Figure 8.39(b). As the milk retailer will be using a large number of such cartons, there is a requirement to use the design that is least expensive to produce. In particular the retailer desires the design that minimizes the amount of waxed cardboard used.

Figure 8.39

Transcribed Image Text:

f(b) = (4b+x)| 1136 000 b2 2x) +b+2x