Starting at the point (x₀, y₀) = (1, 0), a sequence of right-angled triangles is constructed as shown in Figure 2.111. Show that the coordinates of the vertices satisfy the recurrence relations

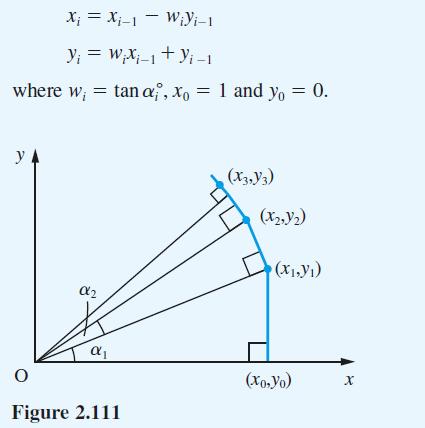
Any angle 0°

where tan Φ_i° = 10^–i and n_i is a non-negative integer. Express θ = 56.5 in this form and, using the recurrence relations above, calculate sin θ° and cos θ° to 5dp. (This method of calculating the trigonometric functions is used in some calculators.)

Transcribed Image Text:

X = X-1 - WYi-1 Yi Y = WX-1 + Y-1 where w = tan a, xo y 2 O Figure 2.111 1 and yo = 0. (X3,Y3) (X2,Y) (X,Y) (xo, Yo) X