Suppose that X is a continuous random variable with mean X and variance 2 X. By separating the integral in the definition of

Suppose that X is a continuous random variable with mean μ_X and variance σ²X. By separating the integral in the definition of σ²X into three parts and substituting the respective bounds for (x – μ_X)² as follows

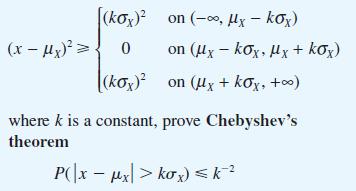
Deduce that for every continuous random variable X the probability is at least 8/9 that X will take a value within three standard deviations of the mean.

(x-x) = [(kOx)2 0 (kox) on (o, Uy kox) on (lx kx, Ux+kOx) on (x + kx, +) where k is a constant, prove Chebyshev's theorem P(x x|> kox) k -