The second-order, linear, nonhomogeneous constant-coefficient differential equation

(often referred to as a forced harmonic oscillator) has a response

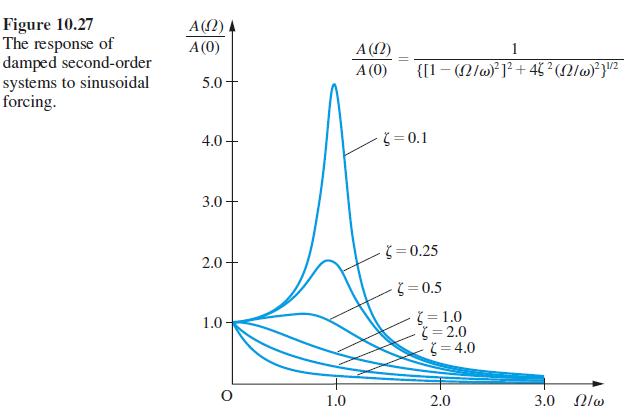
is often called the frequency response (strictly it is the amplitude response or gain spectrum) and is given by (10.55) and shown in Figure 10.27. How does the frequency response of the second-order, nonlinear, nonhomogeneous constant-coefficient differential equation

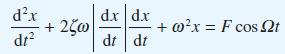
differ from that of the linear one?

Equation 10.55

Transcribed Image Text:

dx dt dx dt + 250- + @x = F cos t