Let 1 and 2 denote the mean weights for animals of two different species. A

Let θ₁ and θ₂ denote the mean weights for animals of two different species. A biologist wishes to estimate the ratio θ₁/θ₂. Unfortunately the species are extremely rare, so the estimate will be based on finding a single animal of each species. Let X_i denote the weight of the species i animal (i = 1, 2), assumed to be normally distributed with mean θ_i and standard deviation 1.

a.

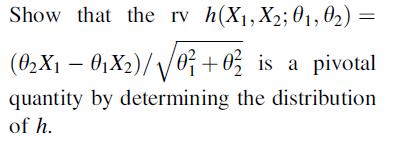
b. Show that h depends on θ₁ and θ₂ only through θ₁/θ₂.

c. Consider Expression (8.7) from the first section of this chapter with a = −1.96 and b = 1.96. Now replace < by = and solve for θ₁/θ₂. Then show that a confidence interval results if x²₁ + x²₂ 1.962, whereas if this inequality is not satisfied, the resulting confidence set is the complement of an interval.

Transcribed Image Text:

Show that the rv h(X₁, X2; 01,02) (0₂X₁ - 0₁X2)/√√0²+02 is a pivotal quantity by determining the distribution of h.