Refer back to the bike helmet data of Exercise 5.

a. Apply Tukey’s procedure at the .05 level to determine which bike helmets have honestly significantly different mean peak linear acceleration under the specified experimental conditions. Use SSE = 3900.
b. Seven of the 10 brands are considered road helmets (elongated shape with aerodynamic venting), while three brands—BMIPS (1), GMIPS (5), and NW (7)—are nonroad helmets. Compute a 95% CI for the contrast 

where the first sum spans across the seven road helmet brands.

Data From Exercise 5

The article “Differences in Impact Performance of Bicycle Helmets During Oblique Impacts” (J. Biomech. Engr. 2018) describes an experiment in which 10 different bicycle helmet brands (4 of each brand, for 40 total helmets) were strapped onto a mannequin head and subjected to a frontal impact at 6.6m/s. At that speed, concussion without a helmet is extremely likely. The peak linear acceleration (PLA, in g) was measured in each test; values over 300 g are associated with a high risk of brain injury.

The sample mean PLAs for the 10 helmet brands are presented below; labels are abbreviations used in the article for the brand names.

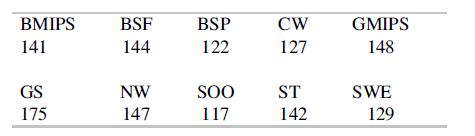
Use these sample means to determine SSTr and MSTr.

The value SSE = 3900 is consistent with information provided in the article.

Construct an ANOVA table, and carry out a hypothesis test at the .01 significance level.

Transcribed Image Text:

0 = // (1²₂ + + M₁0) (μ₁ + M₁ + μ7)