Regression through the origin. Let x denote  the number of items in an order and y denote time (min) necessary to process the order. Processing time may be determined by various factors other than order size. So for any particular value of x, we now regard the value of total production time as a random variable Y. Consider the following data obtained by specifying various values of x and determining total production time for each one.

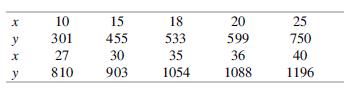
a. Plot the observed (x, y) pairs on a twodimensional coordinate system. Do all points fall exactly on a line passing through (0, 0)? Do the points tend to fall close to such a line?
b. Consider the following probability model for the data. Values x₁, x₂, …, x_n
are specified, and at each x_i we will observe a value of the dependent variable Y_i. Assume that the Y₁,......,Y_n are independent and normally distributed, with Y_i having mean value βx_i and variance σ². That is, rather than assume that y = βx, a linear function of x passing through the origin, we are assuming that the mean value of Y is a linear function of x and that the variance of Y is the same for any particular x value. Obtain formulas for the maximum likelihood estimates of β and σ², and then calculate the estimates for the given data. How would you interpret the estimate of β? What value of processing time would you predict when μ = 25?

Transcribed Image Text:

X y x y 10 301 27 810 15 455 30 903 18 533 35 1054 20 599 36 1088 25 750 40 1196