The following proof that the normal pdf integrates to 1 comes courtesy of Professor Robert Young, Oberlin College. Let f(z) denote the standard normal pdf, and consider the function of two variables

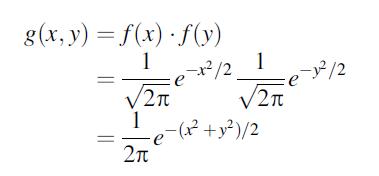
Let V denote the volume under the graph of g(x, y) above the xy-plane.
a. Let A denote the area under the standard normal curve. By setting up the double integral for the volume underneath g(x, y), show that V = A².
b. Using the rotational symmetry of g(x, y), V can be determined by adding up the volumes of shells from rotation about the y-axis:

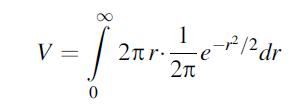
Show this integral equals 1, then use (a) to establish that the area under the standard normal curve is 1.

c. Show that ∫^∞_–∞ƒ (x;μ,σ) dx = 1.

Transcribed Image Text:

g(x, y) = f(x) f(y) 1 -x²/2 || /2π 1 e 2π 1 √2π -(x² +y²)/2 -1²/2