A particle of mass m is in an infinite square well potential given by Since this potential
Question:
A particle of mass m is in an infinite square well potential given by
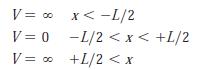
Since this potential is symmetric about the origin, the probability density|Ψ (x)|2 must also be symmetric.
(a) Show that this implies that either Ψ(-x) = Ψ(x) or Ψ(-x) = -Ψ(x).
(b) Show that the proper solutions of the time independent Schrödinger equation can be written
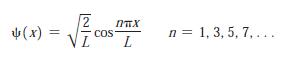
and
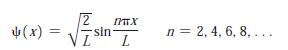
(c) Show that the allowed energies are the same as those for the infinite square well given by Equation 6-24.
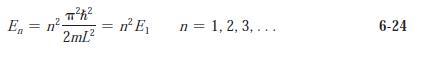
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





