Construct a quark wavefunction for the neutron and proton, and use the results of Problem 9.8 to show that for the ratio of magnetic moments for protons and neutrons, \(\mu_{p} / \mu_{n}=-\frac{3}{2}\), if we approximate \(m_{u}=m_{d}\).

Data from Problem  9.8

If we assume a non-relativistic model, the magnetic moment of a point quark is given by \(\mu_{i}=q_{i} / 2 m_{i}\), where \(q_{i}\) is the charge and \(m_{i}\) the effective mass of quark \(i\). Assume the magnetic moment of the proton to be given by the sum over valence quark contributions

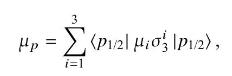
where \(\left|p_{1 / 2}\rightangle\) denotes a proton in the \(M_{J}=J=\frac{1}{2}\) angular momentum state, and \(\sigma_{3}^{i}\) is a Pauli matrix operating on the spin wavefunction of the \(i\) th quark. Use the proton wavefunction constructed to show that the proton magnetic moment is given by \(\mu_{p}=\frac{4}{3} \mu_{u}-\frac{1}{3} u_{d}\), where \(\mu_{u}\) and \(\mu_{d}\) are magnetic moments of the up and down quarks, respectively, and the \(u\) and \(d\) quark masses are assumed equal.

3 Hp = (P1/2 HP1/2), i=1