Evaluate the commutator (left[D_{mu}, D_{v} ight]), where (D_{mu}) is the covariant derivative defined in Eq. (16.36). Show
Question:
Evaluate the commutator \(\left[D_{\mu}, D_{v}\right]\), where \(D_{\mu}\) is the covariant derivative defined in Eq. (16.36). Show that for the U(1) electromagnetic field
\[(i q)^{-1}\left[D_{\mu}, D_{v}\right]=\partial_{\mu} \partial_{v}-\partial_{v} \partial_{\mu}=F_{\mu v}\]
where \(q\) is the gauge coupling strength (gauge charge), \(A_{\mu}\) is the vector field, and \(F_{\mu u}\) is the field strength tensor of Eq. (14.14). Conversely, show that for Yang-Mills gauge fields this commutator suggests the form (16.53) for \(F_{\mu v}\). Operate with the commutator of the covariant derivatives on an arbitrary gauge field \(\Psi\).
Data from Eq. 16.36
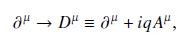
Data from Eq. 14.14
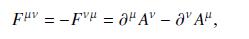
Data from Eq. 16.53
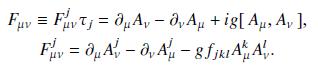
Step by Step Answer:

Symmetry Broken Symmetry And Topology In Modern Physics A First Course
ISBN: 9781316518618
1st Edition
Authors: Mike Guidry, Yang Sun





