If the assumptions leading to the Bose-Einstein distribution are modified so that the number of particles is not assumed constant, the resulting distribution has e^a = 1. This distribution can be applied to a “gas” of photons. Consider the photons to be in a cubic box of side L. The momentum components of a photon are quantized by the standing-wave conditions k_x = n₁π/L, k_y = n₂π/L, k_y = n₂π/L, and k_z = n₃π/L, where p = ћ (k²_x + k²_y + k²_z)1/2 is the magnitude of the momentum. 

(a) Show that the energy of a photon can be written E = N(ћcπ/L), where N² = n²₁ + n²₂ + n²₃. 

(b) Assuming two photons per space state because of the two possible polarizations, show that the number of states between N and N + dN is πN² dN.

(c) Find the density of states and show that the number of photons in the energy interval dE is

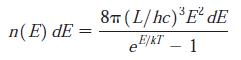
(d) The energy density in dE is given by u(E) dE = En(E) dE/L³. Use this to obtain the Planck blackbody radiation formula for the energy density in dλ, where λ is the wavelength:

n(E) dE= 8T (L/hc)EdE E/KT - 1 e