( mathrm SO (2,1) ) is the analog in two spatial dimensions of the Lorentz group ( mathrm SO (3,1) ) Its generators ( left(X 1 , X 2 , X 3 ight) ) obey the Lie algebra ( left X i , X j ight ) (c i j k X k ) with Use the metric tensor computed from Eq (7 19) to show that ( mathrm SO (2,1) ) is semi...

The Answer is in the image, click to view ...

(mathrm{SO}(2,1)) is the analog in two spatial dimensions of the Lorentz group (mathrm{SO}(3,1)). Its generators (left(X_{1}, X_{2},...

Question:

$\mathrm{SO}(2,1)$ is the analog in two spatial dimensions of the Lorentz group $\mathrm{SO}(3,1)$. Its generators $\left(X_{1}, X_{2}, X_{3}\right)$ obey the Lie algebra $\left[X_{i}, X_{j}\right]=$ $c_{i j}^{k} X_{k}$ with

Use the metric tensor computed from Eq. (7.19) to show that $\mathrm{SO}(2,1)$ is semisimple and non-compact.

Data from Eq. (7.19)

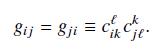
Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For book-img-for-question

Symmetry Broken Symmetry And Topology In Modern Physics A First Course

ISBN: 9781316518618

1st Edition

Authors: Mike Guidry, Yang Sun

See More Books

Question Posted: Mar 28, 2024 02:00 AM

See More Questions

Q1. You have identified a market opportunity for home media players that would cater for older members of the population. Many older people have difficulty in understanding the operating principles...
Portray in words what transforms you would have to make to your execution to some degree (a) to accomplish this and remark on the benefits and detriments of this thought.You are approached to compose...
The following additional information is available for the Dr. Ivan and Irene Incisor family from Chapters 1-5. Ivan's grandfather died and left a portfolio of municipal bonds. In 2012, they pay Ivan...
Dennis Harding is considering acquiring a new automobile that he will use 100% for business. The purchase price of the automobile would be $48,500. If Dennis leased the car for five years, the lease...
Explain the relationships between minitrials and summary jury trials.
Calculating Annuities You have recently won the super jackpot in the Washington State Lottery. On reading the fine print, you discover that you have the following two options: a. You will receive 31...
Is honey a cough remedy? Refer to the Archives of Pediatrics and Adolescent Medicine (Dec. 2007) study of honey as a childrens cough remedy, Exercise 2.40 (p. 79). The data (cough improvement scores)...
1. Describe the experiential learning process that companies mentioned in this case study apply to learn from their mistakes and failures. 2. What perceptual problems do managers need to overcome...
Marcel Company projects the following sales for the first three months of the year: $10,800 in January; $15,900 in February; and $10,400 in March. The company expects 80% of the sales to be cash and...
Show that the Lorentz group commutation relations (13.20) are satisfied by the choices $K_{i}= \pm \frac{i}{2} \sigma_{i}$ and $J_{i}=\frac{1}{2} \sigma_{i}$, where the $\sigma_{i}$ are Pauli...
Prove Eq. (15.30) for massless Poincar particles. Data from Eq. 15.30 W2 == W = WW=-w (P + P).
Explain the basic idea behind the TARP legislation. Was that idea carried out in practice?
Nequired information Exercise 5-17 (Static) Notes receivable-interest accrual and collection LO 5-6 (The following information applies to the questions displayed below) Agrico Incorporated accepted...
Case 14-3 Sarin Pharmaceuticals Ltd. Alan Mannik, director of procurement for the Sarin Phar- maceuticals Ltd. (Sarin) Animal Health Division plant in Vancouver, British Columbia, was planning for...
CL727 LEGAL ANALYSIS AND WRITING Module 11 Assignment: Brief Answer, Analysis, and Conclusion This assignment will be due in Module 11. Your assignment is to write the Brief Answer, Analysis, and...
Question 11 (0.5 points) l) Listen } As a drug manufacturer, you expect your latest wonder drug to lower cholesterol. It has been successful with a limited group of participants so far, so you have...
Redfern Audio produces audio equipment including headphones. At the Campus Facility, it produces two wireless models, Standard and Enhanced, which differ both in the materials and components used and...
In teams of three or four, interview several local businesses to learn what types of complaints they have received regarding defective products. Are these complaints examples of product flaw, failure...
Information graphics, also called infographics, are wildly popular, especially in online environments. Why do you think infographics continue to receive so much attention? How could infographics be...
The Regal Cycle Company manufactures three types of bicyclesa dirt bike, a mountain bike, and a racing bike. Data on sales and expenses for the past quarter follow: Total Dirt Bikes Mountain Bikes...
?? A local college is deciding whether to conduct a campus beautification initiative that would imvolve various projects, such as planting trees and remodeling bulidings, to make the campus more...
A company has net income of $196,000, a profit margin of 9.7 percent, and an accounts receivable balance of $135,370. Assuming 70 percent of sales are on credit, what is the companys days sales in...

(mathrm{SO}(2,1)) is the analog in two spatial dimensions of the Lorentz group (mathrm{SO}(3,1)). Its generators (left(X_{1}, X_{2},...

Question:

[X1, X2] = X3 [X2, X3] = -X1 [X3, X] = X2.

Step by Step Answer:

Symmetry Broken Symmetry And Topology In Modern Physics A First Course

Students also viewed these Sciences questions