Prove that the infinitesimal rank-2 tensor (epsilon_{mu u}) introduced in Eq. (15.7) is antisymmetric in its indices,
Question:
Prove that the infinitesimal rank-2 tensor \(\epsilon_{\mu u}\) introduced in Eq. (15.7) is antisymmetric in its indices, \(\epsilon_{\mu v}=-\epsilon_{v \mu}\), by requiring that Eq. (15.7) be consistent with Eq. (13.24) to first order in \(\epsilon_{\mu u}\).
Data from Eq. 15.7
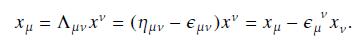
Data from Eq. 13.24
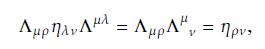
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Symmetry Broken Symmetry And Topology In Modern Physics A First Course
ISBN: 9781316518618
1st Edition
Authors: Mike Guidry, Yang Sun
Question Posted:





