Show that the fermion operator set (left{a, a^{dagger}, a^{dagger} a-frac{1}{2} ight}) obeys and that this is equivalent to the (mathrm{SU}(2)) Lie algebra of Eq. (3.18).

Show that the fermion operator set \(\left\{a, a^{\dagger}, a^{\dagger} a-\frac{1}{2}\right\}\) obeys

and that this is equivalent to the \(\mathrm{SU}(2)\) Lie algebra of Eq. (3.18).

Data from Eq. 3.18

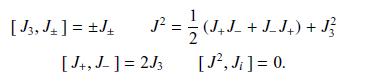
[a,a] = 2(a*a-) [a'a-,a] = ==a [a'a-, a'] = a,