The anomaly $A(R)$ of a fermion representation $R$ is given by [operatorname{Tr}left(left{T^{a}(R), T^{b}(R) ight} T^{c}(R) ight)=frac{1}{2} d^{a
Question:
The anomaly $A(R)$ of a fermion representation $R$ is given by
\[\operatorname{Tr}\left(\left\{T^{a}(R), T^{b}(R)\right\} T^{c}(R)\right)=\frac{1}{2} d^{a b c} A(R)\]
where $T^{a}(R)$ is a representation matrix, the $d^{a b c}$ are totally symmetric constants defined through the anticommutator of the generators as in Eq. (11.17), and $A(R)$ is normalized to unity for the fundamental representation and is independent of the generators. Prove that the $\mathrm{SU}(5)$ representation $\overline{\mathbf{5}} \oplus \mathbf{1 0}$ is anomaly free because the anomalies of the $\overline{\mathbf{5}}$ and $\mathbf{1 0}$ are non-zero, but they exactly cancel each other. Charge $Q$ is a generator so evaluate the above expression for $T^{a}=T^{b}=T^{c}=Q .
Data from Eq. 11.17
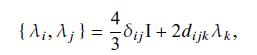
Step by Step Answer:

Symmetry Broken Symmetry And Topology In Modern Physics A First Course
ISBN: 9781316518618
1st Edition
Authors: Mike Guidry, Yang Sun





