Using the commutators for (J_{i}) and (K_{i}) given in Problem 3.8 , argue that the (mathrm{SO}(4)) Lie
Question:
Using the commutators for \(J_{i}\) and \(K_{i}\) given in Problem 3.8 , argue that the \(\mathrm{SO}(4)\) Lie algebra is semisimple, but not simple. Argue that \(\mathrm{SO}(4)\) can be written as a direct product of two simple groups, which can be analyzed independently.
Data from Problem 3.8
Show that for a four-dimensional cartesian space \((x, y, z, t)\) the operators

which is the algebra associated with the group \(\mathrm{SO}(4)\). Show that this \(\mathrm{SO}(4)\) is locally isomorphic to \(\mathrm{SU}(2) \times \mathrm{SU}(2)\) by showing that the new operator set,
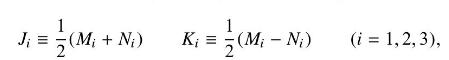
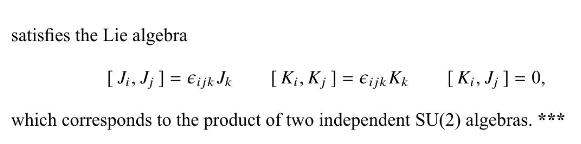
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Symmetry Broken Symmetry And Topology In Modern Physics A First Course
ISBN: 9781316518618
1st Edition
Authors: Mike Guidry, Yang Sun
Question Posted:





