The Hamiltonian matrix for a two-state system can be written as Clearly, the energy eigenfunctions for the
Question:
The Hamiltonian matrix for a two-state system can be written as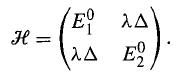
Clearly, the energy eigenfunctions for the unperturbed problems (λ = 0) are given by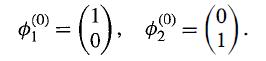
(a) Solve this problem exactly to find the energy eigenfunctions Ψ1 and Ψ2 and the energy eigenvalues E1 and E2.
(b) Assuming that![]() solve the same problem using timeindependent perturbation theory up to first order in the energy eigenfunctions and up to second order in the energy eigenvalues. Compare with the exact results obtained in (a).
solve the same problem using timeindependent perturbation theory up to first order in the energy eigenfunctions and up to second order in the energy eigenvalues. Compare with the exact results obtained in (a).
(c) Suppose the two unperturbed energies are "almost degenerate"; that is,![]()
Show that the exact results obtained in (a) closely resemble what you would expect by applying degenerate perturbation theory to this problem with E01 set exactly equal to E02.
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





