The first three principal components of the yield curve are empirically known to account for almost all of the cross-sectional variation in bond yields. These principal components approximately correspond to the average level, slope, and curvature of the yield curve. Nelson and Siegel (1987) propose the following functional form as an approximation of the yield curve: \({ }^{12}\)

The Nelson-Siegel (NS) specification of the yield curve is a parsimonious approximation of the yield curve that is flexible enough to capture a wide range of observed shapes of the yield curve and has been found to provide a remarkably good fit to the cross-section of yields in many countries. As a result, it is widely used among finance practitioners and central banks.

(a) Plot the loadings of factors \(x_{1 t}, x_{2 t}\), and \(x_{3 t}\) as a function of maturity \(n\) (in months), \(n \geq 1\), for \(\lambda=0.06\). Describe their shapes and their values at \(n=1\) and as \(n ightarrow \infty\). What is the short rate \(y_{1 t}\) and the rate on an infinite-maturity bond, \(\lim _{n ightarrow \infty} y_{n t}\) ?

(b) For each factor, explain whether it mainly affects the short-term, the medium-term, or the long-term component of the yield curve. Explain why \(x_{1 t}, x_{2 t}\), and \(x_{3 t}\) are known, respectively, as the level, slope, and curvature factors of the yield curve. How does the parameter \(\lambda\) affect the role of each factor?

(c) Even though the original NS specification (8.101) does not impose absence of arbitrage, Christensen, Diebold, and Rudebusch (2011) show that, with a small adjustment, the NS yield curve corresponds to a class of arbitrage-free essentially affine three-factor models.
Assume that a state vector \(x_{t}=\left[x_{1 t}, x_{2 t}, x_{3 t}ight]^{\prime}\) evolves under the risk-neutral measure according to

Equation 8.102

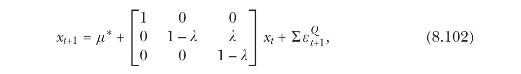
Equation 8.101

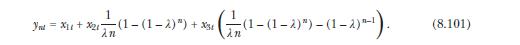
where \(\mu^{*}\) and \(\Sigma\) are unrestricted. Moreover, \(y_{1 t}=x_{1 t}+x_{2 t}\). Use the results of section 8.3.3 to show that under these assumptions the yield curve is given by the NS curve (the right-hand side of (8.101)) plus a maturity-specific constant, \(C_{n}\). Characterize \(C_{n}\).
use the fact that \(x_{1 t}\) in (8.102) follows a random walk, while the evolution of \(x_{2 t}\) and \(x_{3 t}\) does not depend on the level of \(x_{1 t}\).

Data from section 8.3.3

Transcribed Image Text:

in -u (? 1) (u ( 1) 1) 4-7) x + (( 1) 1) 16x +11x = m