Optimal portfolio analysis Consider the following utility function of an investor:

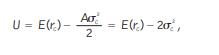
where E(rc ) is the expected rate of return on her complete portfolio (composed of a risky asset and a risk-free asset), C 2 is the variance (the squared standard deviation (volatility) of the complete portfolio), and A is the coefficient of risk aversion:

a What is the coefficient of risk aversion, A, of this particular investor? The expected return on the complete portfolio is given by:

where z is the proportion of the complete portfolio held in the risky asset, which has an expected rate of return, E(rP), of 15 percent, while (1 – z) is the percent held in the risk-free asset, US T-bills. T-bills bear a risk-free rate, rf, of 5 percent. Furthermore, the variance of the risky asset is given by p 2 0.1, or 10 percent.

b Find the optimal proportion of assets held in the risky asset and the proportion held in the risk-free asset. c Compute the expected rate of return on the complete portfolio.

d Compute the variance of the complete portfolio.

e Compute the level of utility (happiness!) of this investor

Transcribed Image Text:

U = E(r.) - AT E(r.)-20% 2