In 1742 the mathematician Christian Goldbach observed that every even number (except 2) seemed representable as the sum of two primes. Goldbach could not prove this result, known today as Goldbach’s conjecture, so he wrote to his friend, the world-famous mathematician Leonhard Euler (see Historical Note on page 766). Euler was unable to prove or disprove this conjecture, and it remains unsolved to this day. Write the following numbers as the sum of two primes (the first three are worked for you):

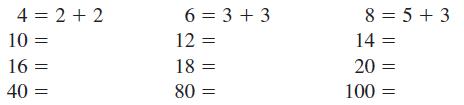
To date, this conjecture has not been proved, but the Russian mathematician L. Schnirelmann (1905–1938) proved that every positive integer can be represented as the sum of not more than 300,000 primes. That may seem like a long way off from Goldbach’s conjecture, but at least 300,000 is a finite number! Later, another mathematician, I. M. Vinogradoff, proved that there exists a number N such that all numbers larger than N can be written as the sum of, at most, four primes.

Transcribed Image Text:

4= 2+2 10 = 16 = 40 = 6=3+3 12 = 18 = 80 = 8=5+3 14 = 20 100 =