Consider the pde for the mean enstrophy obtained in the previous problem. (3.3.1) Solve the pde assuming
Question:
Consider the pde for the mean enstrophy obtained in the previous problem.
(3.3.1) Solve the pde assuming that the vortex stretching term has the form
\[ \left\langle\omega_{\alpha} \omega_{\beta} \frac{\partial v_{\alpha}}{\partial x_{\beta}}\rightangle \approx A e^{\frac{3}{2}} \]
where \(A>0\) is a constant and the initial value \(e(0)>0\) is known.
(3.3.2) Determine the pde for \(\left\langle e^{2}\rightangle\) for 2-d \(\left(v_{3}=0\right)\) homogeneous turbulent flow. Solve the pde for the cases
\[ \frac{1}{R e}\left\langle\frac{\partial \omega_{\alpha}}{\partial x_{\beta}} \frac{\partial \omega_{\alpha}}{\partial x_{\beta}}\rightangle \approx 0 \]
and
\[ \frac{1}{R e}\left\langle\frac{\partial \omega_{\alpha}}{\partial x_{\beta}} \frac{\partial \omega_{\alpha}}{\partial x_{\beta}}\rightangle \approx B \frac{\left\langle e^{2}\rightangle}{\tau} \]
where \(B>0\) and \(\tau>0\) are constants and the initial value \(\left\langle e^{2}\rightangle(0)\) is known.
Problem 3.2
Derive the pde for the dimensionless mean enstrophy \(\left\langle e^{2}\rightangle\) defined by (3.16) in homogeneous turbulence for an incompressible Newtonian fluid with constant viscosity \(\tilde{u}>0\), i.e. \(0
Eq (3.16)
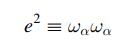
Step by Step Answer:

Navier Stokes Turbulence Theory And Analysis
ISBN: 9783030318697
1st Edition
Authors: Wolfgang Kollmann





