The Hermite functions (Sect. 4.3.3) are a basis for the space (Omega=) (C_{R^{1}}^{infty} cap L_{R^{1}}^{2}) of functions
Question:
The Hermite functions (Sect. 4.3.3) are a basis for the space \(\Omega=\) \(C_{R^{1}}^{\infty} \cap L_{R^{1}}^{2}\) of functions defined on the unbounded domain \(R^{1}\). Determine the coordinates \(c_{i}\) with respect to the basis \(\left\{\Psi_{n}(x): n=0,1, \ldots, \infty\right\}\) of the test function
\[ f(x)=\frac{\cos (k x)}{\sqrt{2 \pi \sigma^{2}}} \exp \left(-\frac{1}{2 \sigma^{2}}\left(x-x_{0}\right)^{2}\right) \]
for \(k=4, x_{0}=0.0\) and \(\sigma=0.5\) as defined in Eq. (4.33) of Sect. 4.3.3. Compute the maximum norm of the error
\[ e(N) \equiv\left|f(x)-\sum_{i=0}^{N} c_{i} \Psi_{i}^{x}\right| \]
as function of \(N\). Plot the coefficients \(c_{i}\), the error \(e(N)\) and the test function compared to the approximation for \(N=20\) terms.
Sect. 4.3.3

Eq. (4.33)
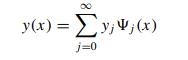
Step by Step Answer:

Navier Stokes Turbulence Theory And Analysis
ISBN: 9783030318697
1st Edition
Authors: Wolfgang Kollmann




