Townsend's model eddy (19.1) is a localized blob of vorticity defined in (mathcal{D}=R^{3}) (Davidson [76], Sect. 6.4.1,
Question:
Townsend's model eddy (19.1) is a localized blob of vorticity defined in \(\mathcal{D}=R^{3}\) (Davidson [76], Sect. 6.4.1, cylindrical coordinates) by \(v_{r}=v_{z}=0\) and
\[ v_{\theta}=\Omega r \exp \left(-2 \frac{\mathbf{x} \cdot \mathbf{x}}{z_{c}^{2}}\right) \]
where \(z_{c}>0\) denotes the eddy length scale and \(\Omega\) is a measure for the angular speed. Assume solenoidal external force, \(abla \cdot \mathbf{G}=\frac{1}{r} \frac{\partial}{\partial r}\left(r G_{r}\right)+\frac{1}{r} \frac{\partial G_{\theta}}{\partial \theta}+\frac{\partial G_{z}}{\partial z}=0\).
(6.1) Compute vorticity in cylindrical coordinates.
(6.2) Split the right-hand side of the pressure pde
\[ \triangle p(\mathbf{x})=2 Q_{A} \]
where \(Q_{A} \equiv-\frac{1}{2} abla \mathbf{v}: abla \mathbf{v}\), into \(Q_{A}=Q_{S}+Q_{W}\). Strain rate and rotation rate tensors are defined by \(\mathbf{s}=\frac{1}{2}\left(\mathbf{A}+\mathbf{A}^{T}\right)\) and \(W=\frac{1}{2}\left(\mathbf{A}-\mathbf{A}^{T}\right)\) and \(Q_{S}=-ho \frac{1}{2} \operatorname{trace}\left(\mathbf{s}^{2}\right)\), \(Q_{W}=-ho \frac{1}{2} \operatorname{trace}\left(\mathbf{W}^{2}\right)\) [13]. Compute the solution of the Poisson pde for \(p\) and separate the contributions of \(Q_{S}\) and \(Q_{W}\). Plot the radial profiles for the azimuthal velocity and enstrophy, the right had sides \(Q_{A}(r, 0), Q_{S}(r, 0), Q_{W}(r, 0)\) and the associated pressure.
Eq (19.1)
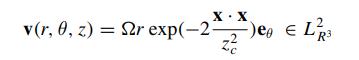
Step by Step Answer:

Navier Stokes Turbulence Theory And Analysis
ISBN: 9783030318697
1st Edition
Authors: Wolfgang Kollmann




