Suppose that the strength of a material is a linear function of two variables (X) and (Y),
Question:
Suppose that the strength of a material is a linear function of two variables \(X\) and \(Y\), as \(S=a X+b Y\). The variables \(X\) and \(Y\) are normally distributed with mean \(\mu_{X}\) and \(\mu_{Y}\) and standard deviation \(\sigma_{X}\) and \(\sigma_{Y}\). Failure is said to occur if \(Z=S-L\). The probability of failure is given by \(P_{f}=\phi(-\beta)\) and \(\beta=\mu_{z} / \sigma_{z}\). Assuming L is deterministic, express \(P_{f}\) in terms of standard deviation of \(X\) and \(Y\).
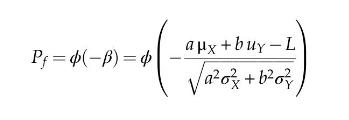
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





