Consider a box of length L = 1 that is initially in contact with a heat reservoir
Question:
Consider a box of length L = 1 that is initially in contact with a heat reservoir on the left at T = 1 and a heat reservoir on the right with T = 0. When this system reaches equilibrium, it will have a temperature distribution T(x) = 1 − x. When the system has equilibrated, the box is disconnected from the heat reservoir and replaced with insulating boundary conditions, ∂T/∂x = 0 at both x = 0 and x = 1. Determine the temperature distribution inside this box, T(x, t) for t > 0 where t = 0 is the time when the boundary conditions change. Since this problem is already stated in a dimensionless form, you can take the heat equation to have the form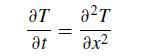
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Numerical Methods With Chemical Engineering Applications
ISBN: 9781107135116
1st Edition
Authors: Kevin D. Dorfman, Prodromos Daoutidis
Question Posted:





