In this problem, you are going to look into the error due to the addition of small numbers and the subtraction of very similar numbers. You should start with the large number x = 10¹⁰. We want to look at different ways to add 1 to this number and then subtract x from the result. If the calculation is perfect, the final result should be 1. If there are round-off errors or chopping errors, you will not get 1.

Define a small number ϵ. In this problem, you will consider the values ϵ = 0.1, 0.01, . . ., 10⁻¹⁰. Your program should perform the following calculation for each value of ϵ,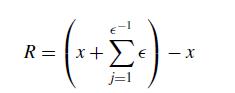

where R is the final result of the calculation. To compute the term in brackets, compute the value of x + ϵ, then add ϵ to that answer to get the value of x + 2ϵ, add ϵ to that answer to get x + 3ϵ, and so on so that computing the term in brackets involves the addition of very different sized numbers. In other words, do not compute the summation and then add it to x. You should not store the value of every step in the calculation – for ϵ = 10⁻¹⁰ this would be a huge memory cost and your program would take a very long time to run. This entire program should execute in less than a minute on a reasonable computer if you write it well. Your program should make a semilogx plot the value of R as a function of ϵ.

Transcribed Image Text:

R = | x + x+Σ j=1 € - *