In this problem, you are going to use RK4 to find the minimum value of the solution of a third-order ordinary differential equation. Consider the solution of the differential equation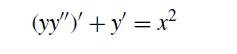

subject to the initial conditions

over the domain x ∈ [0, 1]. You should write a MATLAB program that uses a fourthorder Runge–Kutta integration scheme with step size h = 0.001 to integrate this equation over the domain. You should then compute the minimum value of the function from the information produced by your integration scheme. The minimum value will not occur exactly at one of the time steps, so you will need to use a lever rule or interpolation to find the position of the minimum. Your program should output the minimum value of the function, y_min and the corresponding x value. Make a plot of the function y(x) as a solid line and add the minimum as an open circle. You can do this using the plot command in MATLAB.

Transcribed Image Text:

(vy") + y = x²