Let’s look at another way to compute phase diagrams from an equation of state without using departure functions but still requiring a numerical solution. The van der Waals equation of state can be written in a convenient, dimensionless form as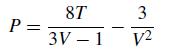

where the reduced pressure is denoted by P ≡ ˆP/P_c, the reduced temperature is denoted by T ≡ ˆT /Tc, and the reduced volume as V ≡ ˆV /V_c, where hats denote real quantities and the subscript cs denote the values at the critical point. These dimensionless quantities will be used from here on forward for ease and clarity of calculation.

Construct a phase diagram for a van der Waals material for values of 0

(a) Start by constructing the phase boundary. There are multiple ways to achieve this, but please use the following. The following conditions must be met along the phase boundary: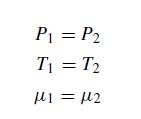

where μ is the chemical potential and 1 and 2 denote the liquid and gas phases respectively.

Consider the thermodynamic relation,

where S is entropy. Along an isotherm (constant T)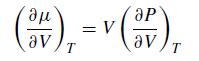

Integrating this equation, substituting the vander Waals equation of state, and evaluating gives

where C(T) is some function of T.

The specific steps for implementation are:

(1) Choose a temperature T^∗

(2) Solve for V₁ and V₂ using the equations along with the specific temperature

(3) use T^∗ along with V₁ or V₂ to solve for P^∗

(4) plot the points (V₁, P^∗) and (V₂, P^∗), on the phase boundary

(5) increment T^∗ to a new value and employ a zeroth-order continuation to solve for the new values of V₁, V₂, and P^∗.

(b) On this phase diagram, plot isotherms corresponding to T = 0.7, 0.8, 0.9, 1, 1.5, 2, 2.5, and 3. Remember that isotherms on the phase diagram should be perfectly straight and horizontal through the two-phase region.

Transcribed Image Text:

P = 87 3V-1 3 V2