42 In this assignment, we will use integer programming and the concept of bond duration to show how Wall Street firms can select an optimal bond portfolio. The duration of a bond (or any stream of payments) is defined as follows: Let C(t) be the payment of the bond at time t (t 1, 2, . . . , n).

Let r market interest rate. If the time-weighted average of the bond’s payments is given by:

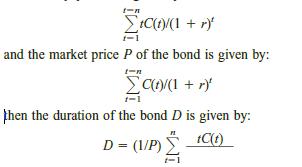
Thus, the duration of a bond measures the “average” time (in years) at which a randomly chosen $1 of NPV is received.
Suppose an insurance company needs to make payments of $20,000 every six months for the next 10 years. If the market rate of interest is 10% per year, then this stream of payments has an NPV of $251,780 and a duration of 4.47 years. If we want to minimize the sensitivity of our bond portfolio to interest risk and still meet our payment obligations, then it has been shown that we should invest $251,780 at the beginning of year 1 in a bond portfolio having a duration equal to the duration of the payment stream.
Suppose the only cost of owning a bond portfolio is the transaction cost associated with the cost of purchasing the bonds. Let’s suppose six bonds are available. The payment streams for these six bonds are given in Table 50. The transaction cost of purchasing any units of bond i equals $500 $5 per bond purchased. Thus, purchasing one unit of bond 1 costs $505 and purchasing 10 units of bond 1 costs $550. Assume that a fractional number of bond i unit purchases is permissible, but in the interests of diversification at most 100 units of any bond can be purchased.
Treasury bonds may also be purchased (with no transaction cost). A treasury bond costs $980 and has a duration of .25 year (90 days).
After computing the price and duration for each bond, use integer programming to determine the immunized bond portfolio that incurs the smallest transaction costs. You may assume the duration of your portfolio is a weighted average of the durations of the bonds included in the portfolio, where the weight associated with each bond is equal to the money invested in that bond.

Transcribed Image Text:

t((1+r) and the market price P of the bond is given by: C(n)/(1+r) then the duration of the bond D is given by: D-(1/P) tC(t)