Consider a maximizing MILP over x1 0, and x2, x3, x4 = 0 or 1. (a)

Consider a maximizing MILP over x1 Ú 0, and x2, x3, x4 = 0 or 1.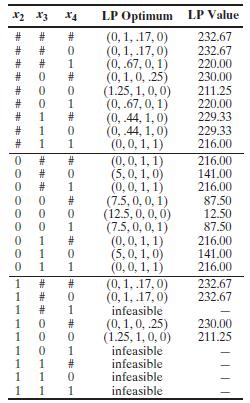

(a) Solve the problem by LP-based Branch and Bound Algorithm 12A, using the given table of candidate problem solutions, and record your computations in a branch and bound tree. When more than one node is active, select the deepest in the tree, breaking ties in favor of the child with newly fixed variable value most like that of its parent’s relaxation optimum. When needed, branch on the fractional variable of the most recent LP relaxation that is closest to integer in value. Start with no incumbent solution, and do not round to create early incumbents.

(b) Briefly explain why the logic of Branch and Bound assures your final solution is optimal.

(c) The table used for part

(a) is a convenience, but really solving the given ILP by branch and bound would have required actually solving a series of candidate problem LP relaxations. How many would have been needed to do the computations of part (a)?

Transcribed Image Text:

23 x4 LP Optimum LP Value # # # # # # # 0 # 0 # 0 # 1 # 1 # 1 0 0 0 ### 0 0 0 0 0 0 0 1 0 1 0 1 1 1 1 10 1 0 ### 10 1 1 1 1 +01+01+01+01+01+01+01+01+0 # (0, 1, .17,0) 232.67 (0, 1, .17,0) 232.67 (0, .67, 0, 1) 220.00 # (0,1,0, .25) 230.00 (1.25,1,0,0) 211.25 (0, .67, 0, 1) 220.00 # (0,.44, 1, 0) 229.33 (0,.44, 1, 0) 229.33 (0,0,1,1) 216.00 # (0, 0, 1, 1) 216.00 (5,0,1,0) 141.00 (0, 0, 1, 1) 216.00 # (7.5,0,0,1) 87.50 (12.5, 0, 0, 0) 12.50 (7.5,0,0,1) 87.50 # (0,0,1,1) 216.00 (5,0,1,0) 141.00 (0,0,1,1) 216.00 # (0,1..17,0) 232.67 (0, 1, .17,0) 232.67 infeasible # (0, 1, 0, .25) 230.00 (1.25, 1, 0, 0) 211.25 infeasible # infeasible infeasible 1 1 1 infeasible