Consider solving the the following minimum total cost facilities location model with Benders Decomposition Algorithm 13E, taking numbers on supply nodes as the fixed cost and capacity (if opened), those on demand nodes as the required inflow, and numbers on arcs as unit costs of transportation.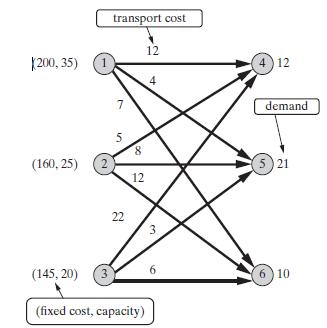

(a) Use nonnegative variables xi, j for flows on arcs (i, j) and binary variables yi = 1 if supply i is opened (= 0 otherwise) to formulate the instance as a capacitated MILP parallel to the uncapacitated one of BG Application 13.5.

(b) Treating y variables as the complicating ones, formulate the corresponding Benders Primal and Benders Dual subproblems (definitions 13.18 and 13.19 ).

(c) Starting with all yi = 1, optimize the instance by Algorithm 13E. Be sure to provide details of sub and master problems solved at each step. Use class optimization software to solve sub and master problems when they become inconvenient for solution by inspection.

Transcribed Image Text:

(200,35) 1 transport cost 12 412 4 7 demand 5 8 (160,25) 2 12 22 22 3 (5)21 6 (145,20) 3 6 10 (fixed cost, capacity)