Return to the Facilities Location Problem (FLP) of Chapter 11, definition 11.29 , and assume all parameters
Question:
Return to the Facilities Location Problem
(FLP) of Chapter 11, definition 11.29 , and assume all parameters are integer.
(a) Consider the following instance: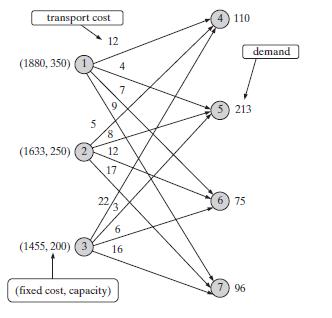
Define a finite alphabet of symbols, and then show a binary encoding of the instance in terms of your alphabet.
(b) Establish that your encoding of
(a) has length proportional to the number of facilities m, demand points n, and the logarithms (rounded up) of objective and constraint coefficients.
(c) State the threshold version 1FLP…2 of the full problem for given threshold v.
(d) Explain why the threshold model of (c)
belongs to class NP but the full optimization model (FLP) does not.
(e) Threshold version 1FLP…2 is known to be NP-Complete. Explain why this implies the full optimization form (FLP) is NP-Hard.
(f) What would be the consequences of discovering a polynomial-time algorithm for either the full optimization model or its threshold analog? Explain.
Step by Step Answer:






