The digraph below shows an instance of the shortest path problem. Numbers on the arcs are lengths. We wish to compute a shortest path from the indicated node s to the indicated node t.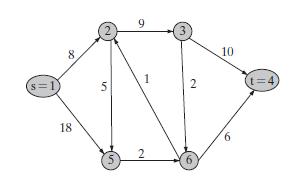

(a) Which of this chapter’s four shortest path Algorithms 9A–9D (Bellman–Ford, Dijkstra, Floyd–Warshall, and Acyclic)
should be preferred for this task? Explain why.

(b) Apply the algorithm recommended in (a)
to compute the lengths of shortest paths from node s to all other nodes. Show all details of labeling and updates as the algorithm proceeds. Then follow that algorithm’s backtrack labels to recover (only)
an optimal path from s to t.

Transcribed Image Text:

s=1 8 9 3 1 5 2 10 t=4 18 2 5 6