Three company trucks must be assigned to pickup 7 miscellaneous loads on the way back from their regular deliveries. Truck capacities and load sizes (cubic yards) are shown in the following table, together with the extra distance (in miles) that each truck would have to travel if it is to deviate to pick up any of the loads.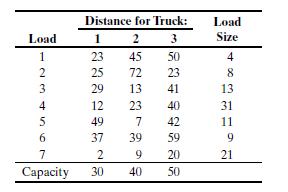

(a) Formulate this problem as a generalized assignment ILP using the decision variables 1i = 1,c, 7; j = 1,c, 32 xi, j ! e 1 if load i goes to truck j 0 otherwise

(b) Enter and use class optimization software to compute an optimal solution.

(c) Use class optimization software to solve the corresponding LP relaxation and verify that the relaxation optimal value provides a lower bound.

(d) Using class optimization software to solve relaxations, verify your ILP optimal solution by executing LP-based branch and bound Algorithm 12A including parent bounds. Apply the depth-first rule for selecting among active nodes and pick whichever of = 0 and = 1 is closest to the preceding relaxation value when nodes have equal depth. Branch on the integer-restricted variable with fractional relaxation value nearest to integer picking the one with least subscript if there are ties. Record incumbent solutions only when an LP relaxation comes out integer (i.e., do not round).

(e) Determine when your search of part (d)
could have been stopped if we were willing to accept an incumbent solution no worse than 25% above optimal.

(f) Do the same branch and bound computation as part

(d) except with the best first enumeration rule using LP relaxation values as parent bounds.
(g) Do the same branch and bound computation as part

(d) except with the depth forward best back enumeration rule using LP relaxation values as parent bounds.
(h) Compare your results in parts (d), (f)
and (g).

Transcribed Image Text:

Distance for Truck: Load Load 1 2 3 Size 1234567 23 45 50 4 25 72 23 8 29 13 41 13 12 23 40 31 49 7 42 11 37 39 59 9 29 20 21 Capacity 30 40 50