A rigid transformation is a mapping from Rⁿ to Rⁿ that is the composition of a translation and a rotation. Mathematically, we can express a rigid transformation Φ  orthogonal transformation and  a vector. 

We are given a set of pairs of pointsand wish to find a rigid transformation that best matches them. We can write the problem as

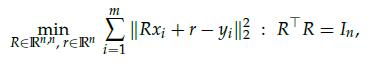
where In is the n x n identity matrix.
The problem arises in image processing, to provide ways to deform an image (represented as a set of two-dimensional points) based on the manual selection of a few points and their transformed counterparts.

1. Assume that R is fixed in problem (5.2). Express an optimal r as a function of R.

2.

3. Show that the problem can be written as

for appropriate matrices X,Y, which you will determine.

4. Show that the problem can be further written as

for an appropriate n x n matrix Z, which you will determine.

5. Show that R = VU^T is optimal, where Z = USV^T is the SVD of Z.

6. Show the result you used in the previous question: assume Z is diagonal, and show that R = In is optimal for the problem above.

7. How woud you apply this technique to make Mona Lisa smile more?

p(x) = Rx+r, where R is an n x n