Consider the problems where f is a convex function, is an arbitrary vector norm, and > 0, > 0 are

Consider the problems

where f is a convex function, ΙΙ · ΙΙ is an arbitrary vector norm, and λ > 0, μ > 0 are parameters. Assume that for every choice of these parameters, the corresponding problems have a unique solution. In general, the solutions for the above problems for fixed λ and μ do not coincide. This exercise shows that we can scan the solutions to the first problem, and get the set of solutions to the second, and vice-versa.

1. Show that both p, q are concave functions, and q̅ with values q̅(μ) = q(1/μ) is convex, on the domain R₊.

2. Show that

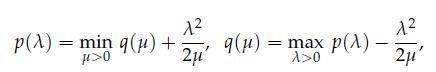
For the second expression, you may assume that dom f has nonempty interior.

3. Deduce from the first part that the path of solutions coincide. That is, if we solve the first problem for every λ > 0, for any μ > 0 the optimal point we thus find will be optimal for the second problem; and vice-versa. It will convenient to denote by x*(λ) (resp. z*(μ)) the (unique) solution to P(λ) (resp. Q(μ)).

4. State and prove a similar result concerning a third function

5. What can you say if we remove the uniqueness assumption?

P(A) P(A) = Q()q(u) = : min f(x) + A||x||, 1 x min f(x) + min f(x) + ||x||, x