Linear dynamical systems are a common way to (approximately) model the behavior of physical phenomena, via recurrence equations of the form²

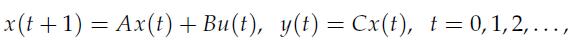
where t is the (discrete) time, x(t) ∈ Rⁿ describes the state of the  system at time t, u(t) ∈ R^p is the input vector, and y(t) ∈ R^m is the  output vector. Here, matrices A, B, C, are given.

1. Assuming that the system has initial condition x(0) = 0, express the output vector at time T as a linear function of u(0), . . . , u( T – 1); that is, determine a matrix H such that y(T) = HU(T), where contains all the inputs up to and including at time T – 1.

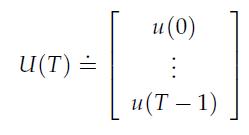2. What is the interpretation of the range of H?

x(t+1) = Ax(t) + Bu(t), y(t) = Cx(t), t=0,1,2,...,