Recall from Exercise 3.11 that a positive matrix A > 0 has a dominant eigenvalue and corresponding left eigenvector > 0 and right eigenvector

Recall from Exercise 3.11 that a positive matrix A > 0 has a dominant eigenvalue and corresponding left eigenvector  ω > 0 and right eigenvector ν > 0 (i.e., ω^TA = λω^T, Aν = λv) which belong to the probability simplex S = {x ∈ Rⁿ : x ≥ 0, 1^Tx = 1}. In this exercise, we shall prove that the dominant eigenvalue has an optimization-based characterization, similar in spirit to the “variational” characterization of the eigenvalues of symmetric matrices. Define the function f : S →R₊₊ with values

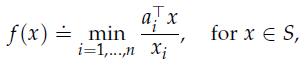
where aT_i is the i-th row of A, and we let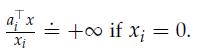

1.Prove that, for all x ∈ S and A > 0, it holds that

2. Prove that

3. Show that f (ν) = λ, and hence conclude that

which is known as the Collatz-Wielandt formula for the dominant eigenvalue of a positive matrix. This formula actually holds more generally for nonnegative matrices27, but you are not asked to prove this fact.

= P(A) > 0,