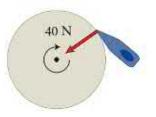
A \(40-\mathrm{kg}\) sharpening wheel of radius \(0.10 \mathrm{~m}\) is rotating at 3.3 revolutions per second. A \(6.0-\mathrm{kg}\) axe is pressed against the rim with a force of \(40 \mathrm{~N}\) directed as shown in Figure P12.87. Treat the wheel as a disk, and assume a coefficient of kinetic friction between wheel and axe blade of \(\mu_{k}=0.35\).

(a) If there is no power source keeping the wheel rotating, how long does it take to stop?

(b) How many revolutions does the wheel make while it is slowing down?

Data from Figure P12.87

Transcribed Image Text:

40 N