(a) For the two-slit barrier shown in Figure P34.13, calculate the angle (theta_{1}) for the first-order bright...
Question:
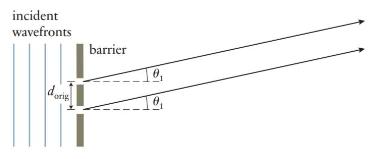
(a) For the two-slit barrier shown in Figure P34.13, calculate the angle \(\theta_{1}\) for the first-order bright fringe if the slit separation distance is \(d_{\text {orig }}=1.0 \mu \mathrm{m}\) and the wavelength of the light passing through the slits is \(546 \mathrm{~nm}\).
(b) Now consider a barrier in which one of the slits oscillates vertically and as a result the slit separation distance varies with time according to \(d(t)=d_{\text {orig }}+A \sin \omega t\). Calculate \(\theta_{1}\) for the first-order bright fringe as a function of time for \(A=0.25 \mu \mathrm{m}\) and \(\omega=100 \mathrm{~s}^{-1}\).
(c) At what instant after \(t=0\) does \(\theta_{1}\) have its maximum value for the first time? What is this maximum value?
(d) At what instant after \(t=0\) does \(\theta_{1}\) have its minimum value for the first time? What is this minimum value?
(e) Which of the parameters \(A, \omega, \lambda, d_{\text {orig }}\) affect the values of these angles?
Data from Figure P34.13
Step by Step Answer:






