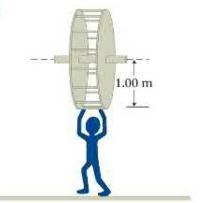
A popular ride at some playgrounds consists of two circular disks joined by rungs (Figure P11.52). The center of the unit is attached to a horizontal axle around which the unit rotates. The rotational inertia of the unit is \(200 \mathrm{~kg} \cdot \mathrm{m}^{2}\), and its radius is \(1.00 \mathrm{~m}\). A \(30.0-\mathrm{kg}\) child runs and grabs the bottom rung of the ride when it is initially at rest. Because the child can pull herself up to meet the rung at waist height, treat her as a particle located on the rung.

(a) If the friction between unit and axle is minimal and can be ignored, what is the minimum speed \(v\) the child must have when she grabs the bottom rung in order to make the unit rotate about its axle and carry her over the top of the unit?

(b) Is this a reasonable speed for a child?

Data from Figure P11.52

Transcribed Image Text:

1.00 m