A small-angle approximation was used to derive Eq. 15. 31, (tau=-(m ell g) vartheta .(a)) What constitutes

Question:

A small-angle approximation was used to derive Eq. 15. 31, $\tau=-(m \ell g) \vartheta .(a)$ What constitutes small in this context? In other words, how large can $\vartheta$ be before it can no longer be called small? (b) As a quantitative benchmark, how large does $\vartheta$ have to be before $(m \ell g) \vartheta$ deviates by more than $1 \%$ from the true value of $\tau$ ?

Data from Eq. 15. 31

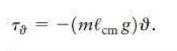
image text in transcribed