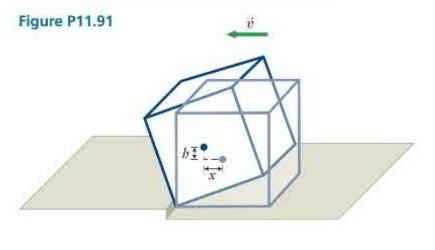
A smooth-faced cube of inertia \(m\) and side length \(d\) sliding along a highly polished floor at speed \(v\) strikes a door threshold, and the collision makes the cube tilt as shown in Figure P11.91. As the cube tips over, its center of mass is located at a variable horizontal distance \(x ; x=0\) when the cube strikes the threshold. What is the rotational speed of the cube as a function of \(x\) ? The rotational inertia of a cube about one edge is \(\frac{2}{3} m d^{2}\). [Call the vertical distance traveled by the center of mass \(h\).]

Data from Figure P11.91

Transcribed Image Text:

Figure P11.91 h