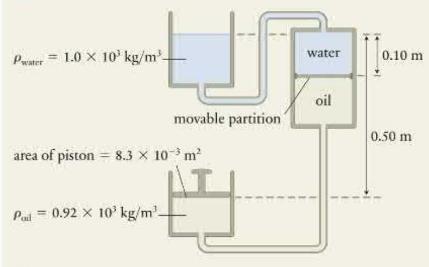
In Figure 18.47, the top tank, which is open to the atmosphere, contains water \(\left(ho_{\text {water }}=1.0 \times 10^{3} \mathrm{~kg} / \mathrm{m}^{3}\right)\) and the bottom tank contains oil \(\left(ho_{\text {oil }}=0.92 \times 10^{3} \mathrm{~kg} / \mathrm{m}^{3}\right)\) covered by a piston. The tank on the right has a freely movable partition that keeps the oil and water separate. The partition is a vertical distance \(0.10 \mathrm{~m}\) below the open surface of the water. If the piston in the bottom tank is \(0.50 \mathrm{~m}\) below the open surface of the water and has a surface area of \(8.3 \times 10^{-3} \mathrm{~m}^{2}\), what must the mass of the piston be to keep the system in mechanical equilibrium? For simplicity, ignore the mass of the partition.

Data from Figure 18.47

Transcribed Image Text:

Peter = 1.010kg/m)_ water 10.10m oil movable partition 0.50m _area of piston = 8.310-3m Paul = 0.9210kg/m_ T