Note in Example 11.10 that the rotational inertia of a thick cylindrical shell is \(\frac{1}{2} m\left(R_{\text {outer }}^{2}+R_{\text {inner }}^{2}\right)\) while that of a solid cylinder is \(\frac{1}{2} m R_{\text {outer }}^{2}\). Does the fact that the factor \(R_{\text {outer }}^{2}+R_{\text {inner }}^{2}\) is larger than the factor \(R_{\text {outer }}^{2}\) mean that you can increase the rotational inertia of a solid cylinder by drilling a hole through it?

Data from Example 11.10

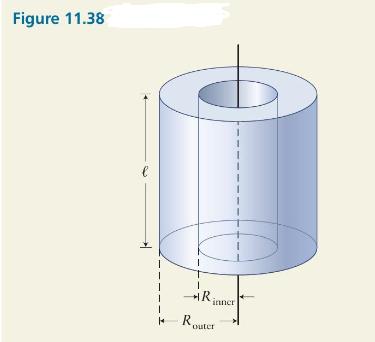
Calculate the rotational inertia of a uniform hollow-core cylinder of inner radius \(R_{\text {inner }}\), outer radius \(R_{\text {outer }}\), length \(\ell\), and inertia \(m\) about an axis parallel to the cylinder's length and passing through its center, as in Figure 11.38.

Transcribed Image Text:

Figure 11.38 e inner R Router