Show that if (f_{1}(x, t)=A_{1} sin left(k_{1} x-omega_{1} t ight)) and (f_{2}(x, t)=) (A_{2} sin left(k_{2} x-omega_{2}
Question:
Show that if \(f_{1}(x, t)=A_{1} \sin \left(k_{1} x-\omega_{1} t\right)\) and \(f_{2}(x, t)=\) \(A_{2} \sin \left(k_{2} x-\omega_{2} t\right)\) are both solutions to the wave equation (Eq. 16. 51), then \(f(x, t)=f_{1}(x, t)+f_{2}(x, t)\) is also a solution.
Data from Eq. 16. 51
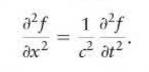
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





